Squaring the circle is but one futile endeavour akin to squeezing a round peg into a square hole. But there are many improbable problems that humanity seeks to solve and with the advent of supercomputers and so-called “big data” it seems that perhaps no problem is now off-limits. Unfortunately, it ain’t necessarily so.
Engineer Chikit Au of the University of Waikato, in Hamilton, New Zealand, has investigated how well we know how to pack circles into a square space and found that although many of us might imagine the answer is obvious, there are many more routes to an apparently optimal solution than one might expect and that there is perhaps no optimal approach to the problem at all. Au suggests that the complexity of the solutions to this purportedly simple puzzle point to an intrinsic truth that complex problems rarely have simple solutions.
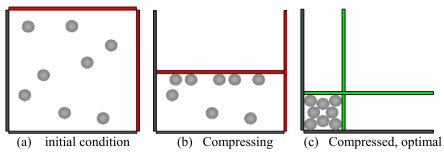
Packing objects has been a perennial problem throughout human history, at least ever since we first grabbed a handful of sticks for the fire or a stash of fruit. It represents an archetypal engineering problem for construction, storage and logistics and in an abstract sense is the archetype of many problems seeking a solution that we face today. Nature, of course, seems to cope with packing very well on its own – think honeycombs and cellular and molecular matrices. Circle cutting to minimise material waste in industry and pie-making alike are examples of packing problems, as too are packing rolls of paper in the publishing industry or pipes in a plumbing warehouse. The list is endless.
Au has carried out a mathematical analysis of the ways – the process from adding the first to the last circle – in which circles can be packed into a square space. There are apparently 27 (not 50) ways that provide an optimal approach to circle packing and 11 pathways that could lead to other optimal approaches to sequential packing of circles. Although it is seemingly a classical problem, Au suggests that circle packing is a much more complex problem than previously thought. The equations that describe the optimal routes and the pathways to other optimal routes to fully packed circles are complicated. Moreover, it seems that optimisation is not affected directly by near neighbours among the circles but how patterns within the layout emerge elsewhere in the arrangement, something that even a supercomputer and huge, let alone big, data cannot yet cope with.
“In the history of science, many attempts, heroic or otherwise, have made on prediction. The science behind the idea is to model the dynamics of the underlying (optimisation) process that give rise to difference equations or differential equations,” says. The “simple” demonstration of the complexity of circle packing suggests a degree of hubris among the scientifically heroic and lessons to be learned for how we approach big problems with big data.
Au, C. (2013) ‘Patterns and pathways of packing circles into a square’, Int J. Computer Applications in Technology, Vol. 48, No. 1, pp. 58—73