History teachers can always turn to the significant figures and battles to enliven their lessons, biology education has the enormously diverse range of species to point to, and even physics can pull in metaphors and anecdotes for the more esoteric aspects, try teaching gravity without mentioning Galileo and the Leaning Tower of Pisa. But, teachers of mathematics have it tough. They can describes solids and shapes, discuss how Alice and Bob might share out an apple pie fairly between nine friends. But. How does one visualise an abstract equation like this:
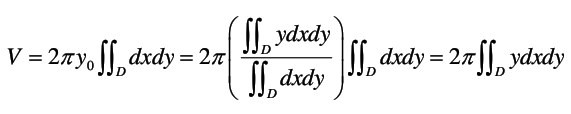
A rare few students will cope entirely, finding a way to see what such a formula means, but most struggle (I know I did) to imagine an object like a four-dimensional hypercube, for instance.
Annunziata Cascone, Gerardo Durazzo, and Valentina Stile of the Department of Information Engineering and Applied Mathematics, at the University of Salerno via Ponte don Melillo, in Italy, point out that mathematics obviously plays an instrumental role in technical degrees, science, engineering, computing etc. Moreover, given how common is the use of computers and calculation programs today in these areas it really is critical that students can get to grips with seemingly esoteric mathematical concepts that have direct application but are hard to visualise.
The team suggests that Computer Algebra Systems (CASs) are the way forward in teaching mathematics for engineering and other technical subjects. Unfortunately, there are many professors who hesitate to use such technologies. They cite technical, personal or even political reasons, Cascone and colleagues explain. “An explanation for such behaviour can be found in the fact that most teachers were not taught to use CASs when they were studying to be teachers,” they say, and so perhaps don’t recognise the enormous possible benefits.
Writing in the International Journal of Knowledge and Learning this month, Cascone and colleagues describe an approach that can effectively integrate CASs into an analysis course, which they say can improve students’ conceptual understanding significantly.
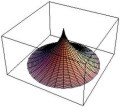
To improve students’ ability to make some geometric concepts concrete, we developed a Mathematica package that is able to realise and visualise the result of a plane domain revolution in a three-dimensional space.
In other words, the package can generate pictures and computations for an equation that would otherwise not have its significant figures, events, battles, and apple pies. “CASs, when used thoughtfully, allow students to concentrate on conceptual development,” the researchers say, “The same students claim that the use of CASs created the possibility of checking their paper-and-pencil results; it enabled them to discover their mistakes and it clarified the processes to solve problems.”
Annunziata Cascone, Gerardo Durazzo, Valentina Stile (2008). Solids by revolution: materialising an idea International Journal of Knowledge and Learning, 4 (2/3) DOI: 10.1504/IJKL.2008.020651